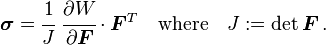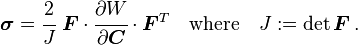Light, Color, Spectra 05/30/2006 Lecture 17 1 Light Color Color Addition & Subtraction Spectra Spring 2006 UCSD: Physics 8; 2006 2 What do we see? • Our eyes can’t detect intrinsic light from objects (mostly t detect intrinsic light from objects (mostly infrared), unless they get “red hot” • The light we see is from the sun or from artificial light • When we see objects, we see reflected light – immediate bouncing of incident light (zero delay) • Very occasionally we see light that has been absorbed, then re-emitted at a different wavelength – called fluorescence, phosphorescence, luminescence Spring 2006 UCSD: Physics 8; 2006 3 Colors • Light is characterized by frequency, or more commonly, by wavelength • Visible light spans from 400 nm to 700 nm – or 0.4 µm to 0.7 µm; 0.0004 mm to 0.0007 mm, etc. Spring 2006 UCSD: Physics 8; 2006 4 White light White light • White light is the combination of all wavelengths, with equal representation – “red hot” poker has much more red than blue light – experiment: red, green, and blue light bulbs make white – RGB monitor combines these colors to display white blue light green light red light wavelength combined, white light called additive color combination—works with light sources Light, Color, Spectra 05/30/2006 Lecture 17 2 Spring 2006 UCSD: Physics 8; 2006 5 Additive Colors Additive Colors • Red, Green, and Blue light sources can be used to synthesize almost any perceivable color • Red + Green = Yellow • Red + Blue = Magenta • Green + Blue = Cyan • These three dual-source colors become the primary colors for subtraction – why? because absence of green is magenta – absence of red is cyan, etc. Spring 2006 UCSD: Physics 8; 2006 6 Subtractive colors Subtractive colors • But most things we see are not light sources • Reflection takes away some of the incident light – thus the term subtractive • If incident light is white, yellow is absence of blue incident white light blue absorption (e.g., paint, dye) reflected yellow light (blue gone) yellow light made of red and green Spring 2006 UCSD: Physics 8; 2006 7 What’s responsible for selective absorption? • Carotene – makes carrots orange, tomatoes red, daffodils yellow, leaves turn – must absorb blue light • Long, organic molecular chain – most dyes, pigments are such – resonances in optical light • Chlorophyll Chlorophyll – makes leaves green – must absorb red and blue Spring 2006 UCSD: Physics 8; 2006 8 Questions Questions • Why, when you mix all your paints together, do you just get dark brown or black? Why not white? • Why is the sky blue, and the low sun/moon orange? Are these related? Light, Color, Spectra 05/30/2006 Lecture 17 3 Spring 2006 UCSD: Physics 8; 2006 9 Our limited sensitivity to light Our limited sensitivity to light • In bright-light situations (called photopic photopic, using cones), our sensitivity peaks around 550 nm, going from 400 to 700 • In the dark, we switch to the dark, we switch to scotopic vision (rods), centered at 510 nm, going from 370 to 630 – it’s why astronomers like red flashlights: don’t ruin night vision Spring 2006 UCSD: Physics 8; 2006 10 Introduction to Spectra • We can make a spectrum out of light, dissecting its constituent colors – A prism is one way to do this – A diffraction grating also does the job • The spectrum represents the wavelength-bywavelength content of light – can represent this in a color graphic like that above – or can plot intensity vs. wavelength – previous plots of blackbody spectrum were of this form Spring 2006 UCSD: Physics 8; 2006 11 Example Spectra Solar Spectrum with Fraunhofer solar atmosphere absorption lines C: Hydrogen; D: Sodium; E: Iron; F: Hydrogen; G: Iron; H&K: Calcium white light spectrum hydrogen lamp spectrum helium lamp spectrum lithium lamp spectrum mercury lamp spectrum hydrogen absorption spectrum Spectra provide “fingerprints” of atomic species, which can be used to identify atoms across the universe! Spring 2006 UCSD: Physics 8; 2006 12 Spectral Content of Light Spectral Content of Light • A spectrum is a plot representing light content on a wavelength-by-wavelength basis – the myriad colors we can perceive are simply different spectral amalgams of light – much like different instruments have different sound: it depends on its (harmonic) spectral content Light, Color, Spectra 05/30/2006 Lecture 17 4 Spring 2006 UCSD: Physics 8; 2006 13 Light Sources Light Sources Here are a variety of light sources. Included are: • H-ITT IR LED* • red LED* • green laser pointer • flourescence of orange H-ITT transmitter illuminated by green laser Note that light has to be blue-ward (shorter wavelength) of the fluorescence for it to work. * LED: Light Emitting Diode Spring 2006 UCSD: Physics 8; 2006 14 Colored Paper Colored Paper Reflected light (in this case, sunlight) off of paper appearing: blue green yellow orange red black aside from slight fluorescence in yellow paper, paper colors operate by reflection only: never peeks above 100% white paper would be a flat line at 100% Spring 2006 UCSD: Physics 8; 2006 15 Fluorescent Paper Fluorescent Paper Bright fluorescent paper follows different rules: absorbs blue or UV light and re-emits at some characteristic wavelength. These examples are of lime green paper and bright orange fluorescent paper. Note especially in the orange case, the light exceeds the amount that would be passively reflected off of white paper (100% level) Spring 2006 UCSD: Physics 8; 2006 16 Fluorescent Markers (hi-lighters) Fluorescent Markers (hi-lighters) Likewise, fluorescent markers (hi-lighters) absorb and re-emit light. In this case, we see yellow, green, and pink fluorescent markers The pink actually has a bit of blue/violet in it, surprisingly All three have emission above the 100% that one gets from straight reflection Light, Color, Spectra 05/30/2006 Lecture 17 5 Spring 2006 UCSD: Physics 8; 2006 17 Fluorescent lights Fluorescent lights • Fluorescent lights stimulate emission among atoms like argon, mercury, neon – they do this by ionizing the gas with high voltage – as electrons recombine with ions, they emit light at discrete wavelengths, or lines • Mercury puts out a strong line at 254 nm (UV) – this and other lines hit the phosphor coating on the inside of the tube and stimulate emission in the visible part of the spectrum Spring 2006 UCSD: Physics 8; 2006 18 LCD Monitor LCD Monitor LCD monitors use fluorescent lights to illuminate the pixels (from behind). The black curve shows what my LCD laptop monitor looks like in a section of the screen that’s white. Blue, green, and red curves show sections of the screen with these colors Note that the colors are achieved simply by suppression Blue gets all of this line Green gets all of this line Red gets all of this line Thus LCDs just filter the background light Spring 2006 UCSD: Physics 8; 2006 19 Transmission of Glass, Sunglasses Transmission of Glass, Sunglasses By obtaining a spectrum of sunlight reflected off of a piece of white paper (using the spectrograph without the fiber feed), then doing the same thing through the fiber and also through sunglasses, the transmission properties of each can be elucidated. The fiber is about 82% transmission for most wavelengths, but has significant UV absorption. This is why you can’t get sunburn through glass The sunglasses block UV almost totally! Spring 2006 UCSD: Physics 8; 2006 20 Sunlight and The Blue Sky Sunlight and The Blue Sky These plots show the spectrograph’s response to sunlight on white paper and to the blue sky. The spectrograph is not very efficient in UV or IR, and its sensitivity curve is shown in black. You can notice the violet hump in the blue sky (brighter than white paper here). Also, can see the solar atmosphere absorption lines in both sun and sky sodium hydrogen oxygen in earth atmos. calcium hydrogen Light, Color, Spectra 05/30/2006 Lecture 17 6 Spring 2006 UCSD: Physics 8; 2006 21 Blackbody corrected The spectrograph software lets you claim a source to be a blackbody of specified temperature, so it can correct for its efficiency curve (black curve on prev.). Here we see the result of this process, which has made the sun curve look like a perfect blackbody peaking at 500 nm. But it also assumed that Fraunhoffer lines were artifacts to be removed Note the dramatic rise of the sky toward the blue/UV end. The lighter blue is without the UV-absorbing fiber in place Spring 2006 UCSD: Physics 8; 2006 22 More realistic spectrum Correcting the raw spectra from two slides back with the response curve, we arrive at a more realistic sun and sky spectrum. The black line is a blackbody at 5900 K, which fits the sun reasonably well. This time, the absorption lines survive. The blue sky now also looks smoother, and on top of this is plotted a theoretical 1/4 model for molecular scattering Though not in words, this explains why the sky is blue! Spring 2006 UCSD: Physics 8; 2006 23 How do diffraction gratings work? • A diffraction grating is a regular array of optical a regular array of optical scattering points – spherical wave emerges from each scattering point – constructively or destructively interfere at different angles depending on wavelength Spring 2006 UCSD: Physics 8; 2006 24 Another look at diffraction gratings Another look at diffraction gratings • For a given wavelength, a special angle will result in constructive interference: d sin = – this angle is different for different wavelengths Light, Color, Spectra 05/30/2006 Lecture 17 7 Spring 2006 UCSD: Physics 8; 2006 25 Assignments Assignments • HW 7: 14.E.8, 14.E.19, 14.E.20, 14.E.21, 15.E.26 – plus additional required problems on website, accessible through Assignments link • Read pp. 446–447, 454–455 to accompany this lecture • Read pp. 447–453 for Thursday, 6/1 • Extra Credit posted on course website – worth up to 3% of grade!!! – mostly involves building a spectrometer and exploring lots of things with it.
Featured post
Wednesday, 20 April 2016
Compilation for Light in Physics
Light, Color, Spectra 05/30/2006 Lecture 17 1 Light Color Color Addition & Subtraction Spectra Spring 2006 UCSD: Physics 8; 2006 2 What do we see? • Our eyes can’t detect intrinsic light from objects (mostly t detect intrinsic light from objects (mostly infrared), unless they get “red hot” • The light we see is from the sun or from artificial light • When we see objects, we see reflected light – immediate bouncing of incident light (zero delay) • Very occasionally we see light that has been absorbed, then re-emitted at a different wavelength – called fluorescence, phosphorescence, luminescence Spring 2006 UCSD: Physics 8; 2006 3 Colors • Light is characterized by frequency, or more commonly, by wavelength • Visible light spans from 400 nm to 700 nm – or 0.4 µm to 0.7 µm; 0.0004 mm to 0.0007 mm, etc. Spring 2006 UCSD: Physics 8; 2006 4 White light White light • White light is the combination of all wavelengths, with equal representation – “red hot” poker has much more red than blue light – experiment: red, green, and blue light bulbs make white – RGB monitor combines these colors to display white blue light green light red light wavelength combined, white light called additive color combination—works with light sources Light, Color, Spectra 05/30/2006 Lecture 17 2 Spring 2006 UCSD: Physics 8; 2006 5 Additive Colors Additive Colors • Red, Green, and Blue light sources can be used to synthesize almost any perceivable color • Red + Green = Yellow • Red + Blue = Magenta • Green + Blue = Cyan • These three dual-source colors become the primary colors for subtraction – why? because absence of green is magenta – absence of red is cyan, etc. Spring 2006 UCSD: Physics 8; 2006 6 Subtractive colors Subtractive colors • But most things we see are not light sources • Reflection takes away some of the incident light – thus the term subtractive • If incident light is white, yellow is absence of blue incident white light blue absorption (e.g., paint, dye) reflected yellow light (blue gone) yellow light made of red and green Spring 2006 UCSD: Physics 8; 2006 7 What’s responsible for selective absorption? • Carotene – makes carrots orange, tomatoes red, daffodils yellow, leaves turn – must absorb blue light • Long, organic molecular chain – most dyes, pigments are such – resonances in optical light • Chlorophyll Chlorophyll – makes leaves green – must absorb red and blue Spring 2006 UCSD: Physics 8; 2006 8 Questions Questions • Why, when you mix all your paints together, do you just get dark brown or black? Why not white? • Why is the sky blue, and the low sun/moon orange? Are these related? Light, Color, Spectra 05/30/2006 Lecture 17 3 Spring 2006 UCSD: Physics 8; 2006 9 Our limited sensitivity to light Our limited sensitivity to light • In bright-light situations (called photopic photopic, using cones), our sensitivity peaks around 550 nm, going from 400 to 700 • In the dark, we switch to the dark, we switch to scotopic vision (rods), centered at 510 nm, going from 370 to 630 – it’s why astronomers like red flashlights: don’t ruin night vision Spring 2006 UCSD: Physics 8; 2006 10 Introduction to Spectra • We can make a spectrum out of light, dissecting its constituent colors – A prism is one way to do this – A diffraction grating also does the job • The spectrum represents the wavelength-bywavelength content of light – can represent this in a color graphic like that above – or can plot intensity vs. wavelength – previous plots of blackbody spectrum were of this form Spring 2006 UCSD: Physics 8; 2006 11 Example Spectra Solar Spectrum with Fraunhofer solar atmosphere absorption lines C: Hydrogen; D: Sodium; E: Iron; F: Hydrogen; G: Iron; H&K: Calcium white light spectrum hydrogen lamp spectrum helium lamp spectrum lithium lamp spectrum mercury lamp spectrum hydrogen absorption spectrum Spectra provide “fingerprints” of atomic species, which can be used to identify atoms across the universe! Spring 2006 UCSD: Physics 8; 2006 12 Spectral Content of Light Spectral Content of Light • A spectrum is a plot representing light content on a wavelength-by-wavelength basis – the myriad colors we can perceive are simply different spectral amalgams of light – much like different instruments have different sound: it depends on its (harmonic) spectral content Light, Color, Spectra 05/30/2006 Lecture 17 4 Spring 2006 UCSD: Physics 8; 2006 13 Light Sources Light Sources Here are a variety of light sources. Included are: • H-ITT IR LED* • red LED* • green laser pointer • flourescence of orange H-ITT transmitter illuminated by green laser Note that light has to be blue-ward (shorter wavelength) of the fluorescence for it to work. * LED: Light Emitting Diode Spring 2006 UCSD: Physics 8; 2006 14 Colored Paper Colored Paper Reflected light (in this case, sunlight) off of paper appearing: blue green yellow orange red black aside from slight fluorescence in yellow paper, paper colors operate by reflection only: never peeks above 100% white paper would be a flat line at 100% Spring 2006 UCSD: Physics 8; 2006 15 Fluorescent Paper Fluorescent Paper Bright fluorescent paper follows different rules: absorbs blue or UV light and re-emits at some characteristic wavelength. These examples are of lime green paper and bright orange fluorescent paper. Note especially in the orange case, the light exceeds the amount that would be passively reflected off of white paper (100% level) Spring 2006 UCSD: Physics 8; 2006 16 Fluorescent Markers (hi-lighters) Fluorescent Markers (hi-lighters) Likewise, fluorescent markers (hi-lighters) absorb and re-emit light. In this case, we see yellow, green, and pink fluorescent markers The pink actually has a bit of blue/violet in it, surprisingly All three have emission above the 100% that one gets from straight reflection Light, Color, Spectra 05/30/2006 Lecture 17 5 Spring 2006 UCSD: Physics 8; 2006 17 Fluorescent lights Fluorescent lights • Fluorescent lights stimulate emission among atoms like argon, mercury, neon – they do this by ionizing the gas with high voltage – as electrons recombine with ions, they emit light at discrete wavelengths, or lines • Mercury puts out a strong line at 254 nm (UV) – this and other lines hit the phosphor coating on the inside of the tube and stimulate emission in the visible part of the spectrum Spring 2006 UCSD: Physics 8; 2006 18 LCD Monitor LCD Monitor LCD monitors use fluorescent lights to illuminate the pixels (from behind). The black curve shows what my LCD laptop monitor looks like in a section of the screen that’s white. Blue, green, and red curves show sections of the screen with these colors Note that the colors are achieved simply by suppression Blue gets all of this line Green gets all of this line Red gets all of this line Thus LCDs just filter the background light Spring 2006 UCSD: Physics 8; 2006 19 Transmission of Glass, Sunglasses Transmission of Glass, Sunglasses By obtaining a spectrum of sunlight reflected off of a piece of white paper (using the spectrograph without the fiber feed), then doing the same thing through the fiber and also through sunglasses, the transmission properties of each can be elucidated. The fiber is about 82% transmission for most wavelengths, but has significant UV absorption. This is why you can’t get sunburn through glass The sunglasses block UV almost totally! Spring 2006 UCSD: Physics 8; 2006 20 Sunlight and The Blue Sky Sunlight and The Blue Sky These plots show the spectrograph’s response to sunlight on white paper and to the blue sky. The spectrograph is not very efficient in UV or IR, and its sensitivity curve is shown in black. You can notice the violet hump in the blue sky (brighter than white paper here). Also, can see the solar atmosphere absorption lines in both sun and sky sodium hydrogen oxygen in earth atmos. calcium hydrogen Light, Color, Spectra 05/30/2006 Lecture 17 6 Spring 2006 UCSD: Physics 8; 2006 21 Blackbody corrected The spectrograph software lets you claim a source to be a blackbody of specified temperature, so it can correct for its efficiency curve (black curve on prev.). Here we see the result of this process, which has made the sun curve look like a perfect blackbody peaking at 500 nm. But it also assumed that Fraunhoffer lines were artifacts to be removed Note the dramatic rise of the sky toward the blue/UV end. The lighter blue is without the UV-absorbing fiber in place Spring 2006 UCSD: Physics 8; 2006 22 More realistic spectrum Correcting the raw spectra from two slides back with the response curve, we arrive at a more realistic sun and sky spectrum. The black line is a blackbody at 5900 K, which fits the sun reasonably well. This time, the absorption lines survive. The blue sky now also looks smoother, and on top of this is plotted a theoretical 1/4 model for molecular scattering Though not in words, this explains why the sky is blue! Spring 2006 UCSD: Physics 8; 2006 23 How do diffraction gratings work? • A diffraction grating is a regular array of optical a regular array of optical scattering points – spherical wave emerges from each scattering point – constructively or destructively interfere at different angles depending on wavelength Spring 2006 UCSD: Physics 8; 2006 24 Another look at diffraction gratings Another look at diffraction gratings • For a given wavelength, a special angle will result in constructive interference: d sin = – this angle is different for different wavelengths Light, Color, Spectra 05/30/2006 Lecture 17 7 Spring 2006 UCSD: Physics 8; 2006 25 Assignments Assignments • HW 7: 14.E.8, 14.E.19, 14.E.20, 14.E.21, 15.E.26 – plus additional required problems on website, accessible through Assignments link • Read pp. 446–447, 454–455 to accompany this lecture • Read pp. 447–453 for Thursday, 6/1 • Extra Credit posted on course website – worth up to 3% of grade!!! – mostly involves building a spectrometer and exploring lots of things with it.
compilation for Electric current
Electric Current (I) The rate of flow of charge through any
cross-section of a wire is called electric current flowing through it. Electric
current (I) = q / t. Its SI unit is ampere (A). The conventional direction of
electric current is the direction of motion of positive charge. The current is
the same for all cross-sections of a conductor of non-uniform cross-section.
Similar to the water flow, charge flows faster where the conductor is smaller
in cross-section and slower where the conductor is larger in cross-section, so
that charge rate remains unchanged. If a charge q revolves in a circle with
frequency f, the equivalent current, i = qf (In a metallic conductor current
flows due to motion of free electrons while in electrolytes and ionized gases
current flows due to electrons and positive ions.) Types of Electric Current
According to its magnitude and direction electric current is of two types (i)
Direct Current (DC) Its magnitude and direction do not change with time. A
ceil, battery or DC dynamo are the sources of direct current. (ii) Alternating
Current (AC) An electric current whose magnitude changes continuously and
changes its direction periodically is called alternating current. AC dynamo is
source of alternating current. Current Density The electric current flowing per
unit area of cross-section of conductor is called current density. Current
density (J) = I / A Its S1 unit is ampere metre-2 and dimensional formula is
[AT-2 ]. It is a vector quantity and its direction is in the direction of motion
positive charge or in the direction of flow of current. Thermal Velocity of
Free Electrons 2 | P a g e www.ncerthelp.com (Visit for all ncert solutions in
text and videos, CBSE syllabus, note and many more) Free electrons in a metal
move randomly with a very high speed of the order of 105 ms-1. This speed is
called thermal velocity of free electron. Average thermal velocity of free
electrons in any direction remains zero. Drift Velocity of Free Electrons When
a potential difference is applied across the ends of a conductor, the free
electrons in it move with an average velocity opposite to direction of electric
field. which is called drift velocity of free electrons. Drift velocity vd =
eEτ / m = eVτ / ml where, τ = relaxation time, e = charge on electron, E =
electric field intensity, 1 = length of the conductor, V = potential difference
across the ends of the conductor m = mass of electron. Relation between
electric current and drift velocity is given by vd = I / An e Mobility The
drift velocity of electron per unit electric field applied is mobility of
electron. Mobility of electron (μ) = vd / E Its SI unit is m2 s -1V -1 and its
dimensional formula is [M-1T 2A]. Ohm’s Law If physical conditions of a
conductor such as temperature remains unchanged, then the electric current (I)
flowing through the conductor is directly proportional to the potential
difference (V) applied across its ends. I ∝ V
or V = IR where R is the electrical resistance of the conductor and R = Ane2 τ
/ ml. Electrical Resistance 3 | P a g e www.ncerthelp.com (Visit for all ncert
solutions in text and videos, CBSE syllabus, note and many more) The
obstruction offered by any conductor in the path of flow of current is called
its electrical resistance. Electrical resistance, R = V / I Its SI unit is ohm
(Ω) and its dimensional formula is [ML2T -3A -2 ]. Electrical resistance of a
conductor R = ρl / A where, l = length of the conductor, A = cross-section area
and ρ = resistivity of the material of the conductor. Resistivity Resistivity
of a material of a conductor is given by ρ = m / n2 τ where, n = number of free
electrons per unit volume. Resistivity of a material depend on temperature and
nature of the material. It is independent of dimensions of the conductor, i.e.,
length, area of cross-section etc. Resistivity of metals increases with
increase in temperature as ρt = ρo (1 + αt) where ρo and ρt are resistivity of
metals at O°C and t°C and α temperature coefficient of resistivity of the
material. For metals α is positive, for some alloys like nichrome, manganin and
constantan, α is positive but very low. For semiconductors and insulators. α is
negative. Resistivity is low for metals, more for semiconductors and very high
alloys like nichrome, constantan etc. (In magnetic field the resistivity of
metals increases. But resistivity of ferromagnetic materials such as iron,
nickel, cobalt etc decreases in magnetic field.) Electrical Conductivity The
reciprocal of resistivity is called electrical conductivity. 4 | P a g e
www.ncerthelp.com (Visit for all ncert solutions in text and videos, CBSE
syllabus, note and many more) Electrical conductivity (σ) = 1 / ρ = 1 / RA =
ne2 τ / m Its SI units is ohm-1 m -1 or mho m-1 or siemen m-1 . Relation
between current density (J) and electrical conductivity (σ) is given by J = σ E
where, E = electric field intensity. Ohmic Conductors Those conductors which
obey Ohm’s law, are called ohmic conductors e.g., all metallic conductors are
ohmic conductor. For ohmic conductors V – I graph is a straight line. Non-ohmic
Conductors Those conductors which do not obey Ohm’s law, are called non-ohmic
conductors. e.g., diode valve, triode valve, transistor , vacuum tubes etc. For
non-ohmic conductors V – I graph is not a straight line. Superconductors When
few metals are cooled, then below a certain critical temperature their
electrical resistance suddenly becomes zero. In this state, these substances
are called superconductors and this phenomena is calledsuperconductivity.
Mercury become superconductor at 4.2 K, lead at 7.25 K and niobium at 9.2 K 5 |
P a g e www.ncerthelp.com (Visit for all ncert solutions in text and videos,
CBSE syllabus, note and many more) Colour Coding of Carbon Resistors The
resistance of a carbon resistor can be calculated by the code given on it in the
form of coloured strips. Colour coding Colour Figure Black 0 Brown 1 Red 2
Orange 3 Yellow 4 Green 5 Blue 6 Violet 7 Grey 8 White 9 Tolerance power Colour
Tolerance Gold 5% Silver 10% No colour 20% This colour coding can be easily
learned in the sequence “B B ROY Great Bratain Very Good Wife”. Combination of
Resistors 1.In Series (i) Equivalent resistance, R = R1 + R2 + R3 (ii) Current
through each resistor is same. 6 | P a g e www.ncerthelp.com (Visit for all
ncert solutions in text and videos, CBSE syllabus, note and many more) (iii)
Sum of potential differences across individual resistors is equal to the
potential difference, applied by the source. 2. In Parallel Equivalent
resistance 1 / R = 1 /R1 + 1 / R2 + 1 / R3 Potential difference across each resistor
is same. Sum of electric currents flowing through individual resistors is equal
to the be electric current drawn from the source. Electric Cell An electric
cell is a device which converts chemical energy into electrical energy.
Electric cells are of two types (i) Primary Cells Primary ceUs cannot be
charged again. Voltic, Daniel and Leclanche cells are primary cells. (ii)
Secondary Cells Secondary cells can be charged again and again. Acid and alkali
accumulators are secondary cells. Electro – motive – Force (emf) of a Cell The
energy given by a cell in flowing unit positive charge throughout the circuit
completely one time, is equal to the emf of a cell. Emf of a cell (E) = W / q.
Its SI unit is volt. Terminal Potential Difference of a Cell 7 | P a g e www.ncerthelp.com
(Visit for all ncert solutions in text and videos, CBSE syllabus, note and many
more) The energy given by a cell in flowing unit positive charge through till
outer circuit one time from one terminal of the cell to the other terminal of the
cell. Terminal potential difference (V) = W / q. Its SI unit is volt. Internal
Resistance of a Cell The obstruction offered by the electrolyte of a cell in
the path of electric current is called internal resistance (r) of the cell.
Internal resistance of a cell (i) Increases with increase in concentration of
the electrolyte. (ii) Increases with increase in distance between the
electrodes. (iii) Decreases with increase in area of electrodes dipped in
electrolyte. Relation between E. V and r E = V + Ir r = (E / V – 1) R If cell
is in charging state, then E = V – Ir Grouping of Cells (i) In Series If n
cells, each of emf E and internal resistance r are connected in series to a
resistance R. then equivalent emf Eeq = E1 + E2 + …. + En = nE Equivalent
internal resistance req = r1 + r2 + …. + rn = nr Current In the circuit I = Eeq
/ (R + req) = nE / (R + nr) (ii) In Parallel If n cells. each of emf E and
internal resistance r are connected to in parallel. then equivalent emf. Eeq =
E 8 | P a g e www.ncerthelp.com (Visit for all ncert solutions in text and
videos, CBSE syllabus, note and many more) Equivalent internal resistance 1 /
req = 1 / r1 + 1 / r1 + … + 1 / rn = n / r or req = r / n Current In the
circuit I = E / (R + r / n) (iii) Mixed Grouping of Cells If n cells, each of
emf E and internal resistance r are connected in series and such m rows are
connected in parallel, then Equivalent emf, Eeq Equivalent Internal resistance
req Current in the circuit, I = nE / (R + nr / m) or I = mnE / mR + nr
Monday, 18 April 2016
compilation for study of elasticity
ELASTICITY: FROM https://en.wikipedia.org/wiki/Elasticity_%28physics%29
In physics, elasticity (from Greek ἐλαστός "ductible") is the ability of a body to resist a distorting influence or stress and to return to its original size and shape when the stress is removed. Solid objects will deform when forces are applied on them. If the material is elastic, the object will return to its initial shape and size when these forces are removed.
The physical reasons for elastic behavior can be quite different for different materials. In metals, the atomic lattice changes size and shape when forces are applied (energy is added to the system). When forces are removed, the lattice goes back to the original lower energy state. For rubbers and other polymers, elasticity is caused by the stretching of polymer chains when forces are applied.
Perfect elasticity is an approximation of the real world, and few materials remain purely elastic even after very small deformations. In engineering, the amount of elasticity of a material is determined by two types of material parameter. The first type of material parameter is called a modulus, which measures the amount of force per unit area (stress) needed to achieve a given amount of deformation. The units of modulus are pascals (Pa) or pounds of force per square inch (psi, also lbf/in2). A higher modulus typically indicates that the material is harder to deform. The second type of parameter measures the elastic limit. The limit can be a stress beyond which the material no longer behaves elastic and deformation of the material will take place. If the stress is released, the material will elastically return to a permanent deformed shape instead of the original shape.
When describing the relative elasticities of two materials, both the modulus and the elastic limit have to be considered. Rubbers typically have a low modulus and tend to stretch a lot (that is, they have a high elastic limit) and so appear more elastic than metals (high modulus and low elastic limit) in everyday experience. Of two rubber materials with the same elastic limit, the one with a lower modulus will appear to be more elastic.
Overview When an elastic material is deformed due to an external force, it experiences internal resistance to the deformation and restores it to its original state if the external force is no longer applied. There are various elastic moduli, such as Young's modulus, the shear modulus, and the bulk modulus, all of which are measures of the inherent elastic properties of a material as a resistance to deformation under an applied load. The various moduli apply to different kinds of deformation. For instance, Young's modulus applies to extension/compression of a body, whereas the shear modulus applies to its shear.[1]
The elasticity of materials is described by a stress-strain curve, which shows the relation between stress (the average restorative internal force per unit area) and strain (the relative deformation).[2] The curve is generally nonlinear, but it can (by use of a Taylor series) be approximated as linear for sufficiently small deformations (in which higher-order terms are negligible). If the material is isotropic, the linearized stress-strain relationship is called Hooke's law, which is often presumed to apply up to the elastic limit for most metals or crystalline materials whereas nonlinear elasticity is generally required to model large deformations of rubbery materials even in the elastic range. For even higher stresses, materials exhibit plastic behavior, that is, they deform irreversibly and do not return to their original shape after stress is no longer applied.[3] For rubber-like materials such as elastomers, the slope of the stress-strain curve increases with stress, meaning that rubbers progressively become more difficult to stretch, while for most metals, the gradient decreases at very high stresses, meaning that they progressively become easier to stretch.[4] Elasticity is not exhibited only by solids; non-Newtonian fluids, such as viscoelastic fluids, will also exhibit elasticity in certain conditions quantified by the Deborah number. In response to a small, rapidly applied and removed strain, these fluids may deform and then return to their original shape. Under larger strains, or strains applied for longer periods of time, these fluids may start to flow like a viscous liquid.
Because the elasticity of a material is described in terms of a stress-strain relation, it is essential that the terms stress and strain be defined without ambiguity. Typically, two types of relation are considered. The first type deals with materials that are elastic only for small strains. The second deals with materials that are not limited to small strains. Clearly, the second type of relation is more general in the sense that it must include the first type as a special case.
For small strains, the measure of stress that is used is the Cauchy stress while the measure of strain that is used is the infinitesimal strain tensor; the resulting (predicted) material behavior is termed linear elasticity, which (for isotropic media) is called the generalized Hooke's law. Cauchy elastic materials and hypoelastic materials are models that extend Hooke's law to allow for the possibility of large rotations, large distortions, and intrinsic or induced anisotropy.
For more general situations, any of a number of stress measures can be used, and it generally desired (but not required) that the elastic stress-strain relation be phrased in terms of a finite strain measure that is work conjugate to the selected stress measure, i.e., the time integral of the inner product of the stress measure with the rate of the strain measure should be equal to the change in internal energy for any adiabatic process that remains below the elastic limit.
Linear elasticity
Main article: Linear elasticity
As noted above, for small deformations, most elastic materials such as springs
exhibit linear elasticity and can be described by a linear relation
between the stress and strain. This relationship is known as Hooke's law. A geometry-dependent version of the idea[5] was first formulated by Robert Hooke in 1675 as a Latin anagram, "ceiiinosssttuv". He published the answer in 1678: "Ut tensio, sic vis" meaning "As the extension, so the force",[6][7][8] a linear relationship commonly referred to as Hooke's law. This law can be stated as a relationship between tensile force F and corresponding extension displacement x, :
:Although the general proportionality constant between stress and strain in three dimensions is a 4th-order tensor called stiffness, systems that exhibit symmetry, such as a one-dimensional rod, can often be reduced to applications of Hooke's law.
Finite elasticity
The elastic behavior of objects that undergo finite deformations has been described using a number of models, such as Cauchy elastic material models, Hypoelastic material models, and Hyperelastic material models. The deformation gradient (F) is the primary deformation measure used in finite strain theory.Cauchy elastic materials
Main article: Cauchy elastic material
A material is said to be Cauchy-elastic if the Cauchy stress tensor σ is a function of the deformation gradient F alone:Even though the stress in a Cauchy-elastic material depends only on the state of deformation, the work done by stresses might depend on the path of deformation. Therefore, Cauchy elasticity includes non-conservative "non-hyperelastic" models (in which work of deformation is path dependent) as well as conservative "hyperelastic material" models (for which stress can be derived from a scalar "elastic potential" function).
Hypoelastic materials
Main article: Hypoelastic material
A hypoelastic material can be rigorously defined as one that is modeled using a constitutive equation satisfying the following two criteria:[9]1. The Cauchy stress
 at time
at time 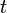 depends only on the order in which the body has occupied its past
configurations, but not on the time rate at which these past
configurations were traversed. As a special case, this criterion
includes a Cauchy elastic material, for which the current stress depends only on the current configuration rather than the history of past configurations.
depends only on the order in which the body has occupied its past
configurations, but not on the time rate at which these past
configurations were traversed. As a special case, this criterion
includes a Cauchy elastic material, for which the current stress depends only on the current configuration rather than the history of past configurations.2. There is a tensor-valued function
 such that
such that 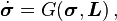 in which
in which  is the material rate of the Cauchy stress tensor, and
is the material rate of the Cauchy stress tensor, and  is the spatial velocity gradient tensor.
is the spatial velocity gradient tensor.If only these two original criteria are used to define hypoelasticity, then hyperelasticity would be included as a special case, which prompts some constitutive modelers to append a third criterion that specifically requires a hypoelastic model to not be hyperelastic (i.e., hypoelasticity implies that stress is not derivable from an energy potential). If this third criterion is adopted, it follows that a hypoelastic material might admit nonconservative adiabatic loading paths that start and end with the same deformation gradient but do not start and end at the same internal energy.
Note that the second criterion requires only that the function
 exists. As detailed in the main Hypoelastic material article, specific formulations of hypoelastic models typically employ so-called objective rates so that the
exists. As detailed in the main Hypoelastic material article, specific formulations of hypoelastic models typically employ so-called objective rates so that the  function exists only implicitly and is typically needed explicitly only
for numerical stress updates performed via direct integration of the
actual (not objective) stress rate.
function exists only implicitly and is typically needed explicitly only
for numerical stress updates performed via direct integration of the
actual (not objective) stress rate.Hyperelastic materials
Main article: Hyperelastic material
Hyperelastic materials (also called Green elastic materials) are conservative models that are derived from a strain energy density function (W). A model is hyperelastic if and only if it is possible to express the Cauchy stress tensor as a function of the deformation gradient via a relationship of the form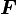 ). By also requiring satisfaction of Objectivity (frame invariance), the energy potential may be alternatively regarded as a function of the Cauchy-Green deformation tensor (
). By also requiring satisfaction of Objectivity (frame invariance), the energy potential may be alternatively regarded as a function of the Cauchy-Green deformation tensor ( ), in which case the hyperelastic model may be written alternatively as
), in which case the hyperelastic model may be written alternatively asApplications
Linear elasticity is used widely in the design and analysis of structures such as beams, plates and shells, and sandwich composites. This theory is also the basis of much of fracture mechanics.Hyperelasticity is primarily used to determine the response of elastomer-based objects such as gaskets and of biological materials such as soft tissues and cell membranes.
Factors affecting elasticity
For isotropic materials, the presence of fractures affects the Young and the shear modulus perpendicular to the planes of the cracks, which decrease (Young's modulus faster than the shear modulus) as the fracture density increases,[10] indicating that the presence of cracks makes bodies brittler. Microscopically, the stress-strain relationship of materials is in general governed by the Helmholtz free energy, a thermodynamic quantity. Molecules settle in the configuration which minimizes the free energy, subject to constraints derived from their structure, and, depending on whether the energy or the entropy term dominates the free energy, materials can broadly be classified as energy-elastic and entropy-elastic. As such, microscopic factors affecting the free energy, such as the equilibrium distance between molecules, can affect the elasticity of materials: for instance, in inorganic materials, as the equilibrium distance between molecules at 0 K increases, the bulk modulus decreases.[11] The effect of temperature on elasticity is difficult to isolate, because there are numerous factors affecting it. For instance, the bulk modulus of a material is dependent on the form of its lattice, its behavior under expansion, as well as the vibrations of the molecules, all of which are dependent on temperature.[12]compilation for study of circular motion
ircular Motion : Ref http://www.askiitians.com/iit-jee-physics/mechanics/circular-motion.aspx

Now we shall discuss another example of two-dimensional motion that is motion of a particle on a circular path. This type of motion is called circular motion.The motion of a body is said to be circular if it moves in such a way that its distance from a certain fixed point always remains the same.
Consider a particle P is moving on circle of radius r on X-Y plane with origin O as centre.
The position of the particle at a given instant may be described by angle θ, called angular position of the particle, measured in radian. As the particle moves on the path, its angular position θ changes. The rate of change of angular position is called angular velocity, ω, measured in radian per second.

= dθ/dt = ds/rdt = v/r
The rate of change of angular velocity is called angular acceleration, measured in rad/s2. Thus, the angular acceleration is
α = dω/dt = d2θ/dt2

It is easy to derive the equations of rotational kinematics for the case of constant angular acceleration with fixed axis of rotation. These equations are of the same form as those for on-dimensional transitional motion.
(a) What is the angular velocity of the minute and hour hands of a clock?
(b) Suppose the clock starts malfunctioning at 7 AM which decelerates the minute hand at the rate of 4Π radians/day. How much time would the clock loose by 7 AM next day?
Solution:-
(a) Angular speed of,
minute hand : ωmh = 2π rad/hr = 48π rad/day = (Π/1800) rad/sec
hour hand : ωhh = (π/6) rad/hr = 4π rad/day = (Π/21600) rad/sec
(b) Assume at t = 0, ?0 = 0, when the clock begins to malfunction.
Use equation (ii) to get the angle covered by the minute hand in one day.
So, ? = ω0(1 day) 1/2α(1 day)2 = 46π rad
Hence the minute hand complete 23 revolutions, so the clock losses 1 hour.
Problem 2:
A particle is rotating in a circular path having initial angular velocity 5 rad/sec and the angular acceleration α = 0.5 ω, where ω is angular velocity at that instant. Find the angular velocity, after it moved an angle π?
Solution:-
Here angular acceleration is
α = 0.5 ω
=> dω/dt = 0.5ω
=> (dω/dθ) (dθ/dt) = 0.5ω
=> ω dω/dθ = 0.5ω
Or,

=> ω - 5 = 0.5 × π
=> ω = 5 + 0.5 ×π = 6.57 rad/sec.
Hence, when acceleration is not constant, use the method of calculus as shown in above illustration
Uniform circular motion assumes that an object is moving (1) in circular motion, and (2) at constant speed  ; then
; then

where r is the radius of the circular path, and is the time period for one revolution.
is the time period for one revolution.
Any object travelling on a circle will return to its original starting point in the period of one revolution, T. At this point the object has travelled a distance . If T is the time that it takes to travel distance 2πr then the object's speed is
. If T is the time that it takes to travel distance 2πr then the object's speed is

where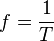

where θ is the angular coordinate of the object (see the diagram on the right-hand side for reference).
Since the speed in uniform circular motion is constant, it follows that

From that fact, a number of useful relations follow:

The equations that relate how θ changes with time are analogous to those of linear motion at constant speed. In particular,

The angle at ,
, 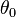 , is commonly referred to as phase.
, is commonly referred to as phase.
Now we shall discuss another example of two-dimensional motion that is motion of a particle on a circular path. This type of motion is called circular motion.The motion of a body is said to be circular if it moves in such a way that its distance from a certain fixed point always remains the same.
Direction of motion of body at any instant:-
If the string breaks suddenly, the stone shall fly tangentially to the path of motion. So, instantaneous direction of motion of the body is always along the tangent to the curve at that point.Consider a particle P is moving on circle of radius r on X-Y plane with origin O as centre.
The position of the particle at a given instant may be described by angle θ, called angular position of the particle, measured in radian. As the particle moves on the path, its angular position θ changes. The rate of change of angular position is called angular velocity, ω, measured in radian per second.
= dθ/dt = ds/rdt = v/r
The rate of change of angular velocity is called angular acceleration, measured in rad/s2. Thus, the angular acceleration is
α = dω/dt = d2θ/dt2
Relation between These Parameters:-
It is easy to derive the equations of rotational kinematics for the case of constant angular acceleration with fixed axis of rotation. These equations are of the same form as those for on-dimensional transitional motion.
ω = ω0 + αt ............ (a)
? = ?0 + ω0t + αt2/2 ............ (b)
ω2 = ω02 + 2α (? - ?0) ............ (c)
? = ?0 + (ω0 + ω)/(2t) ............ (d)
Here, ?0 is the initial angle and ω0 is the initial angular speed.
Problem 1:(a) What is the angular velocity of the minute and hour hands of a clock?
(b) Suppose the clock starts malfunctioning at 7 AM which decelerates the minute hand at the rate of 4Π radians/day. How much time would the clock loose by 7 AM next day?
Solution:-
(a) Angular speed of,
minute hand : ωmh = 2π rad/hr = 48π rad/day = (Π/1800) rad/sec
hour hand : ωhh = (π/6) rad/hr = 4π rad/day = (Π/21600) rad/sec
(b) Assume at t = 0, ?0 = 0, when the clock begins to malfunction.
Use equation (ii) to get the angle covered by the minute hand in one day.
So, ? = ω0(1 day) 1/2α(1 day)2 = 46π rad
Hence the minute hand complete 23 revolutions, so the clock losses 1 hour.
Problem 2:
A particle is rotating in a circular path having initial angular velocity 5 rad/sec and the angular acceleration α = 0.5 ω, where ω is angular velocity at that instant. Find the angular velocity, after it moved an angle π?
Solution:-
Here angular acceleration is
α = 0.5 ω
=> dω/dt = 0.5ω
=> (dω/dθ) (dθ/dt) = 0.5ω
=> ω dω/dθ = 0.5ω
Or,
=> ω - 5 = 0.5 × π
=> ω = 5 + 0.5 ×π = 6.57 rad/sec.
Hence, when acceleration is not constant, use the method of calculus as shown in above illustration
Uniform Circular Motion
from https://en.wikibooks.org/wiki/Physics_Study_Guide/Circular_Motion
Speed and frequency
A two dimensional polar co-ordinate system. The point M can be located in 2D plane as  in Cartesian coordinate system or
in Cartesian coordinate system or  in polar coordinate system
in polar coordinate system
 in Cartesian coordinate system or
in Cartesian coordinate system or  in polar coordinate system
in polar coordinate system ; then
; then
where r is the radius of the circular path, and
 is the time period for one revolution.
is the time period for one revolution.Any object travelling on a circle will return to its original starting point in the period of one revolution, T. At this point the object has travelled a distance
 . If T is the time that it takes to travel distance 2πr then the object's speed is
. If T is the time that it takes to travel distance 2πr then the object's speed is
where
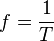
Angular frequency
Uniform circular motion can be explicitly described in terms of polar coordinates through angular frequency, ω:
where θ is the angular coordinate of the object (see the diagram on the right-hand side for reference).
Since the speed in uniform circular motion is constant, it follows that

From that fact, a number of useful relations follow:

The equations that relate how θ changes with time are analogous to those of linear motion at constant speed. In particular,

The angle at
 ,
, 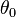 , is commonly referred to as phase.
, is commonly referred to as phase.Velocity, centripetal acceleration and force
The position of an object in a plane can be converted from polar to cartesian coordinates through the equations


Expressing θ as a function of time gives equations for the cartesian coordinates as a function of time in uniform circular motion:


Differentiation with respect to time gives the components of the velocity vector:


Velocity in circular motion is a vector tangential to the trajectory of the object. Furthermore, even though the speed is constant the velocity vector changes direction over time. Further differentiation leads to the components of the acceleration (which are just the rate of change of the velocity components):


The acceleration vector is perpendicular to the velocity and oriented towards the centre of the circular trajectory. For that reason, acceleration in circular motion is referred to as centripetal acceleration.
The absolute value of centripetal acceleration may be readily obtained by


For centripetal acceleration, and therefore circular motion, to be maintained a centripetal force must act on the object. From Newton's Second Law it follows directly that the force will be given by

the components being


and the absolute value


Expressing θ as a function of time gives equations for the cartesian coordinates as a function of time in uniform circular motion:


Differentiation with respect to time gives the components of the velocity vector:


Velocity in circular motion is a vector tangential to the trajectory of the object. Furthermore, even though the speed is constant the velocity vector changes direction over time. Further differentiation leads to the components of the acceleration (which are just the rate of change of the velocity components):


The acceleration vector is perpendicular to the velocity and oriented towards the centre of the circular trajectory. For that reason, acceleration in circular motion is referred to as centripetal acceleration.
The absolute value of centripetal acceleration may be readily obtained by


For centripetal acceleration, and therefore circular motion, to be maintained a centripetal force must act on the object. From Newton's Second Law it follows directly that the force will be given by

the components being


and the absolute value
Subscribe to:
Comments (Atom)