ircular Motion : Ref http://www.askiitians.com/iit-jee-physics/mechanics/circular-motion.aspx
Now we shall discuss another example of two-dimensional motion that is motion of a particle on a circular path. This type of motion is called circular motion.The motion of a body is said to be circular if it moves in such a way that its distance from a certain fixed point always remains the same.
Consider a particle P is moving on circle of radius r on X-Y plane with origin O as centre.
The position of the particle at a given instant may be described by angle θ, called angular position of the particle, measured in radian. As the particle moves on the path, its angular position θ changes. The rate of change of angular position is called angular velocity, ω, measured in radian per second.
= dθ/dt = ds/rdt = v/r
The rate of change of angular velocity is called angular acceleration, measured in rad/s2. Thus, the angular acceleration is
α = dω/dt = d2θ/dt2
It is easy to derive the equations of rotational kinematics for the case of constant angular acceleration with fixed axis of rotation. These equations are of the same form as those for on-dimensional transitional motion.
(a) What is the angular velocity of the minute and hour hands of a clock?
(b) Suppose the clock starts malfunctioning at 7 AM which decelerates the minute hand at the rate of 4Π radians/day. How much time would the clock loose by 7 AM next day?
Solution:-
(a) Angular speed of,
minute hand : ωmh = 2π rad/hr = 48π rad/day = (Π/1800) rad/sec
hour hand : ωhh = (π/6) rad/hr = 4π rad/day = (Π/21600) rad/sec
(b) Assume at t = 0, ?0 = 0, when the clock begins to malfunction.
Use equation (ii) to get the angle covered by the minute hand in one day.
So, ? = ω0(1 day) 1/2α(1 day)2 = 46π rad
Hence the minute hand complete 23 revolutions, so the clock losses 1 hour.
Problem 2:
A particle is rotating in a circular path having initial angular velocity 5 rad/sec and the angular acceleration α = 0.5 ω, where ω is angular velocity at that instant. Find the angular velocity, after it moved an angle π?
Solution:-
Here angular acceleration is
α = 0.5 ω
=> dω/dt = 0.5ω
=> (dω/dθ) (dθ/dt) = 0.5ω
=> ω dω/dθ = 0.5ω
Or,
=> ω - 5 = 0.5 × π
=> ω = 5 + 0.5 ×π = 6.57 rad/sec.
Hence, when acceleration is not constant, use the method of calculus as shown in above illustration
Uniform circular motion assumes that an object is moving (1) in circular motion, and (2) at constant speed 
; then
where r is the radius of the circular path, and
is the time period for one revolution.
Any object travelling on a circle will return to its original starting point in the period of one revolution, T. At this point the object has travelled a distance
. If T is the time that it takes to travel distance 2πr then the object's speed is
where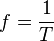
where θ is the angular coordinate of the object (see the diagram on the right-hand side for reference).
Since the speed in uniform circular motion is constant, it follows that
From that fact, a number of useful relations follow:
The equations that relate how θ changes with time are analogous to those of linear motion at constant speed. In particular,
The angle at
, 
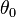, is commonly referred to as phase.
Now we shall discuss another example of two-dimensional motion that is motion of a particle on a circular path. This type of motion is called circular motion.The motion of a body is said to be circular if it moves in such a way that its distance from a certain fixed point always remains the same.
Direction of motion of body at any instant:-
If the string breaks suddenly, the stone shall fly tangentially to the path of motion. So, instantaneous direction of motion of the body is always along the tangent to the curve at that point.Consider a particle P is moving on circle of radius r on X-Y plane with origin O as centre.
The position of the particle at a given instant may be described by angle θ, called angular position of the particle, measured in radian. As the particle moves on the path, its angular position θ changes. The rate of change of angular position is called angular velocity, ω, measured in radian per second.
= dθ/dt = ds/rdt = v/r
The rate of change of angular velocity is called angular acceleration, measured in rad/s2. Thus, the angular acceleration is
α = dω/dt = d2θ/dt2
Relation between These Parameters:-
It is easy to derive the equations of rotational kinematics for the case of constant angular acceleration with fixed axis of rotation. These equations are of the same form as those for on-dimensional transitional motion.
ω = ω0 + αt ............ (a)
? = ?0 + ω0t + αt2/2 ............ (b)
ω2 = ω02 + 2α (? - ?0) ............ (c)
? = ?0 + (ω0 + ω)/(2t) ............ (d)
Here, ?0 is the initial angle and ω0 is the initial angular speed.
Problem 1:(a) What is the angular velocity of the minute and hour hands of a clock?
(b) Suppose the clock starts malfunctioning at 7 AM which decelerates the minute hand at the rate of 4Π radians/day. How much time would the clock loose by 7 AM next day?
Solution:-
(a) Angular speed of,
minute hand : ωmh = 2π rad/hr = 48π rad/day = (Π/1800) rad/sec
hour hand : ωhh = (π/6) rad/hr = 4π rad/day = (Π/21600) rad/sec
(b) Assume at t = 0, ?0 = 0, when the clock begins to malfunction.
Use equation (ii) to get the angle covered by the minute hand in one day.
So, ? = ω0(1 day) 1/2α(1 day)2 = 46π rad
Hence the minute hand complete 23 revolutions, so the clock losses 1 hour.
Problem 2:
A particle is rotating in a circular path having initial angular velocity 5 rad/sec and the angular acceleration α = 0.5 ω, where ω is angular velocity at that instant. Find the angular velocity, after it moved an angle π?
Solution:-
Here angular acceleration is
α = 0.5 ω
=> dω/dt = 0.5ω
=> (dω/dθ) (dθ/dt) = 0.5ω
=> ω dω/dθ = 0.5ω
Or,
=> ω - 5 = 0.5 × π
=> ω = 5 + 0.5 ×π = 6.57 rad/sec.
Hence, when acceleration is not constant, use the method of calculus as shown in above illustration
Uniform Circular Motion
from https://en.wikibooks.org/wiki/Physics_Study_Guide/Circular_Motion
Speed and frequency
A two dimensional polar co-ordinate system. The point M can be located in 2D plane as 
in Cartesian coordinate system or 
in polar coordinate system
in Cartesian coordinate system or in polar coordinate system; thenwhere r is the radius of the circular path, and
is the time period for one revolution.Any object travelling on a circle will return to its original starting point in the period of one revolution, T. At this point the object has travelled a distance
. If T is the time that it takes to travel distance 2πr then the object's speed iswhere
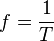
Angular frequency
Uniform circular motion can be explicitly described in terms of polar coordinates through angular frequency, ω:where θ is the angular coordinate of the object (see the diagram on the right-hand side for reference).
Since the speed in uniform circular motion is constant, it follows that
From that fact, a number of useful relations follow:
The equations that relate how θ changes with time are analogous to those of linear motion at constant speed. In particular,
The angle at
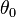, , is commonly referred to as phase.Velocity, centripetal acceleration and force
The position of an object in a plane can be converted from polar to cartesian coordinates through the equations
Expressing θ as a function of time gives equations for the cartesian coordinates as a function of time in uniform circular motion:
Differentiation with respect to time gives the components of the velocity vector:
Velocity in circular motion is a vector tangential to the trajectory of the object. Furthermore, even though the speed is constant the velocity vector changes direction over time. Further differentiation leads to the components of the acceleration (which are just the rate of change of the velocity components):
The acceleration vector is perpendicular to the velocity and oriented towards the centre of the circular trajectory. For that reason, acceleration in circular motion is referred to as centripetal acceleration.
The absolute value of centripetal acceleration may be readily obtained by
For centripetal acceleration, and therefore circular motion, to be maintained a centripetal force must act on the object. From Newton's Second Law it follows directly that the force will be given by
the components being
and the absolute value
Expressing θ as a function of time gives equations for the cartesian coordinates as a function of time in uniform circular motion:
Differentiation with respect to time gives the components of the velocity vector:
Velocity in circular motion is a vector tangential to the trajectory of the object. Furthermore, even though the speed is constant the velocity vector changes direction over time. Further differentiation leads to the components of the acceleration (which are just the rate of change of the velocity components):
The acceleration vector is perpendicular to the velocity and oriented towards the centre of the circular trajectory. For that reason, acceleration in circular motion is referred to as centripetal acceleration.
The absolute value of centripetal acceleration may be readily obtained by
For centripetal acceleration, and therefore circular motion, to be maintained a centripetal force must act on the object. From Newton's Second Law it follows directly that the force will be given by
the components being
and the absolute value
Compilation
ReplyDelete